Weekly Hand Analysis - Mark Olsky - February 12, 2024 - Opening Bid

 

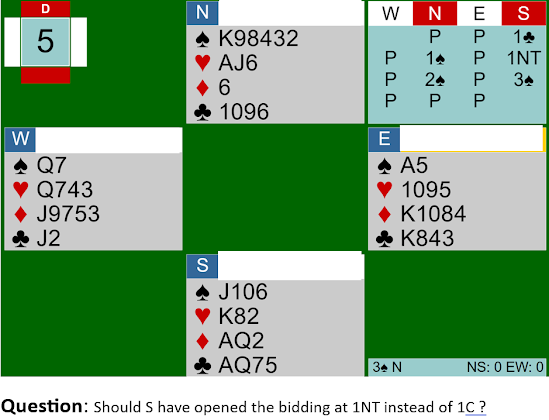
Question:  Should S have opened the bidding at 1NT instead of 1C?

Mark:

Yes! This is a classic 1NT opening. The actual thing that happened, North bidding 1 spade, shows why failing to open 1NT becomes a problem, one that could have been predicted. Now South has a choice of misleading bids, each of which can trap North into going too low or too high. 

  What are South's next options after 1 spade? 1NT ( the actual bid) promises a balanced hand with no more than 14 points. 2NT shows at least 18 points. Both these bids are well wide of the mark. Raising spades is an option, but at the point that partner bids 1 spade there's no way to know that North has anything more than 4 low spades. If you jump to 3 spades initially, you convey the right strength but the wrong length and you could be too high already if partner is at a minimum of both length and strength. 

  In the actual auction, after N bids 2 spades and South raises to 3, North has a tough choice. South has promised a full 14 HCP (remember that the earlier bidding has limited South's points) 2 or 3 spades (Yes, it could be 2 with an honor, since you now know N has 6 of them). Does N have enough to go 4 anyway? I think so, but it's close. That's why if I had to sit in suddenly for South after being handed my first 2 bids, I'd jump to 4 spades. As I lay down the dummy I'd say "Partner, my bidding may be reckless, but this is how highly I think of your play." 4 spades is a slight overbid for South, but not by as much as 3 spades is an underbid. The difference is one huge card on this auction, which carries no high card points but a good probability of being worth an extra trick in the play, the spade 10!

  Re- evaluating the playing potential of a hand is a pretty advanced skill, but you can't advance very far if you can't do it, or give up even trying. 

  As in practically every bidding analysis I submit, I will delve into the play, because the bidding is no more than a systematic and dynamic estimate of what will happen in the play. In this case, the odds heavily favor getting to 4 spades, no less, no more. As it happens, an extremely lucky distribution makes it possible to make 6 spades! At the opposite end of the spectrum, if you got the most unlucky distribution, you'd be undeservedly rewarded for stopping in a part- score.